[LQR] iLQR/DDP algorithm for Non-linear trajectory optimization

Differential Dynamic Programming (DDP) is an indirect method which optimizes over the unconstrained control-space. It uses a 2nd-order Taylor series approximation of the cost-to-go in Dynamic Programming (DP) to compute Newton steps on the control trajectory.

• iLQR: Only keeps the first-order terms (Gauss-Newton approximation), which is similar to Riccati iterations, but accounts for the regularization and line-search required to handle the nonlinearity.
• DDP: Second-order terms included (Newton approximation).

The iLQR/DDP controller solves the following finite-horizon optimization (Non-linear trajectory optimization) problem:

$$ \begin{aligned} \min_{x_{1:N},u_{1:N-1}} \quad & \sum_{i=1}^{N-1} \bigg[ \frac{1}{2} (x_i - {x}_{ref})^TQ({x}_i - {x}_{ref}) + \frac{1}{2} u_i^TRu_i \bigg] + \frac{1}{2}(x_N- {x}_{ref})^TQ_f ({x}_N- {x}_{ref})\\ \text{st} \quad & x_1 = x_{\text{IC}} \\ & x_{i+1} = f(x_i, u_i) \quad \text{for } i = 1,2,\ldots,N-1
\end{aligned} $$

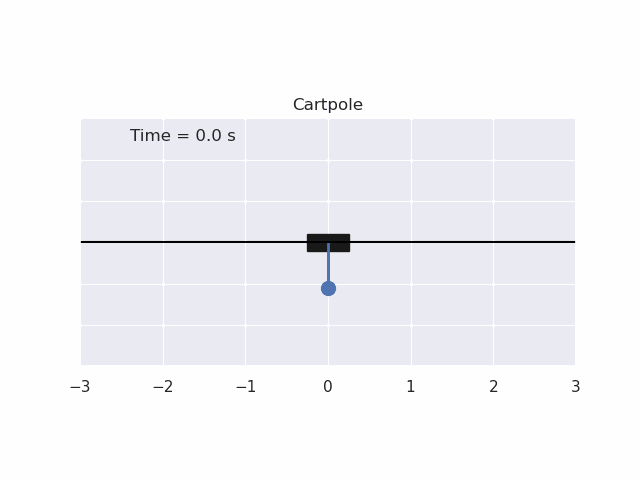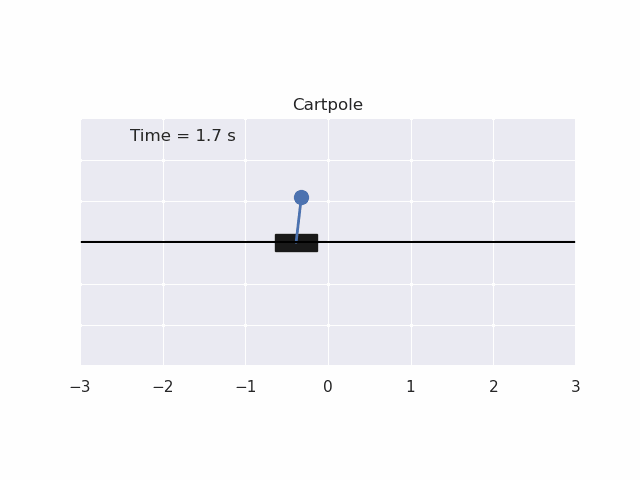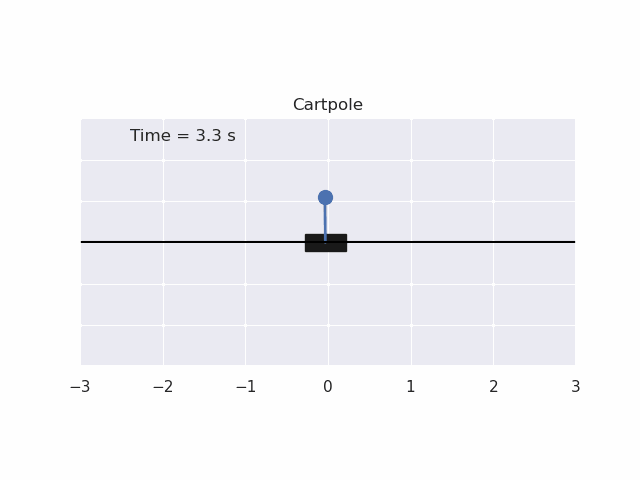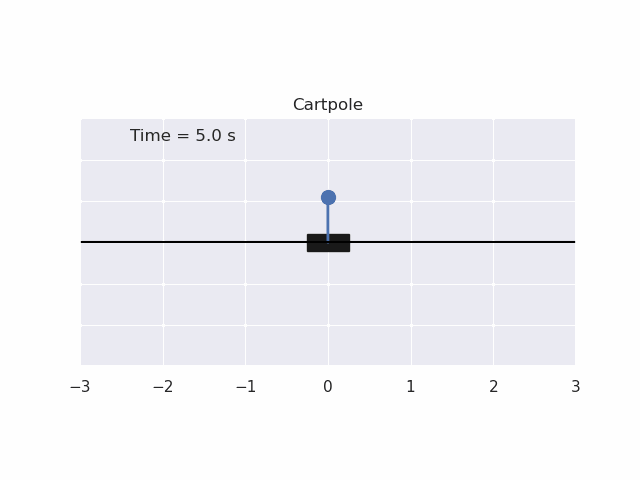
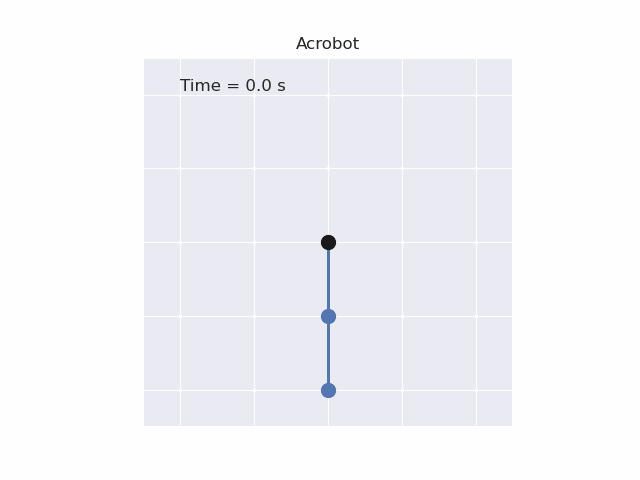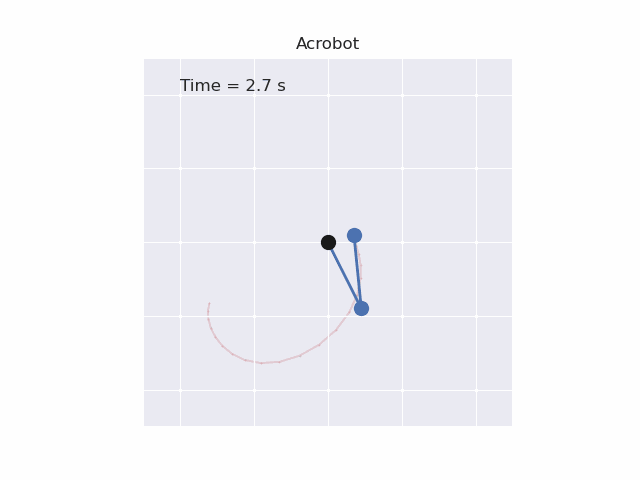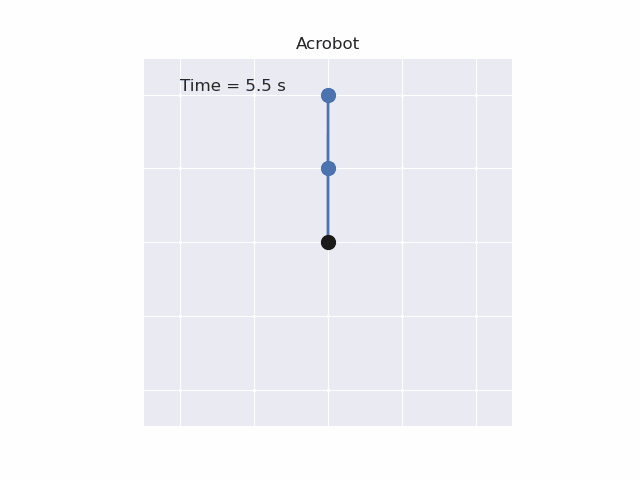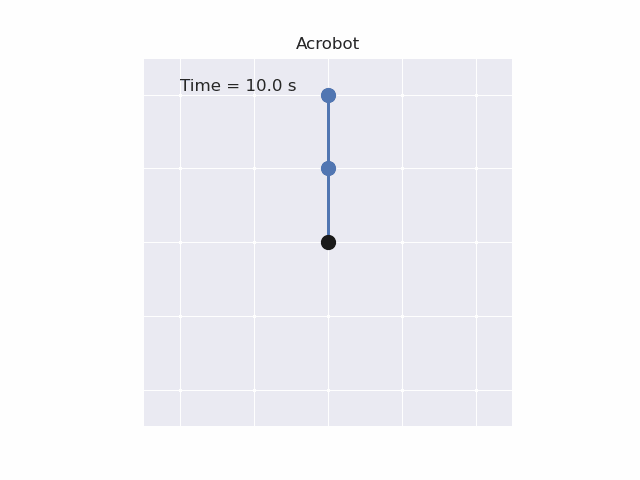
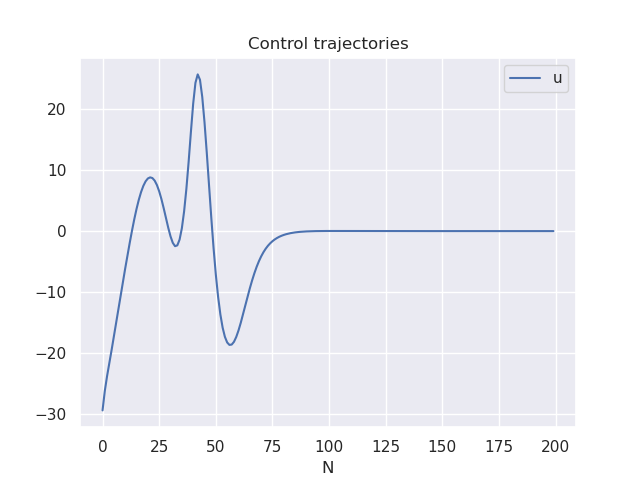
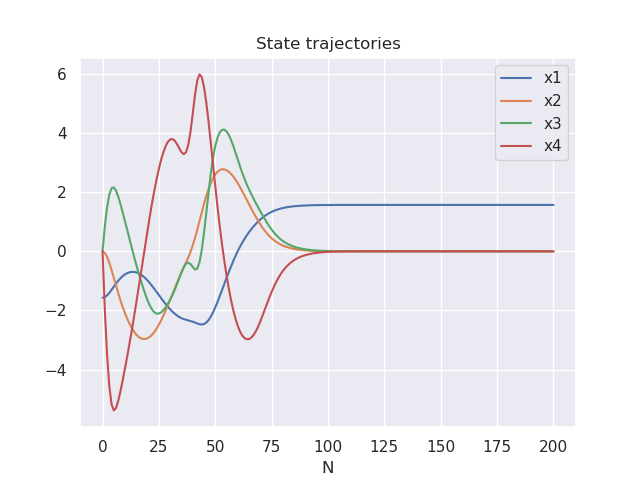
Installation

To use this project, install it locally via:

git clone https://github.com/phatcvo/iLQR-DDP.git

The dependencies can be installed by running:

pip install -r requirements.txt

To execute the code, run:

python3 main.py